Des Statistiques et des Humains
Dès qu'on s'intéresse à l'origine génétique du comportement, on s'aperçoit que beaucoup de commentaires ne sont fondés que sur une mauvaise compréhension de certains concepts statistiques. Cette page n'a donc pour objectif que de les présenter... afin de répondre par avance aux critiques les plus fréquemment lues et entendues.
Sommaire
corrélation ne signifie pas causalité
Dans "Une logique de la communication", Paul Watzlawick raconte que la plus forte corrélation trouvée dans les années 1950 a été celle entre la consommation de bière sur la côte ouest des USA, et la mortalité infantile au Japon. Cet exemple a été fréquemment repris pour montrer les limites des statistiques et faire croire "qu'on peut leur faire dire n'importe quoi". Et en effet beaucoup feront remarquer qu'on ne peut accuser les Américains assoiffés de tuer les Japonais (on remarquera d'ailleurs que personne n'accuse les enfants Japonais de mourir pour assoiffer les Américains).
D'où vient l'erreur ? Et bien c'est tout simple : Corrélation ne signifie pasCausalité. Considérons les termes : quand deux faits apparaissent comme ayant suivi la même progression dans le temps, nous avons une corrélation. Quand un fait a entraîné l'apparition d'un autre nous avons une relation de cause-à-effet, c'est à dire une causalité. Une causalité peut être directe ou indirecte, à plusieurs niveaux, d'une ou plusieurs conséquences qui elles-mêmes peuvent être parralèlesou séquentielles.
Un exemple simple : un accident de voiture peut être la cause directe d'un passage chez le garagiste. Si l'immobilisation du véhicule oblige son possesseur à l'annulation d'un déplacement, ce même accident en sera la cause indirecte, au deuxième degré : les deux conséquences sont séquentielles(accident => Immobilisation => Annulation). Ce même accident peut aussi être la cause directe d'une hospitalisation, et par là-même la cause indirecte d'autres événements (par exemple la rencontre de l'infirmière). Résumons cela dans un tableau :
| Cause Première | ||
| Conséquences 1° | ||
| Conséquences 2° | ||
Nous voyons que l'immobilisation et l'hospitalisation sont deux conséquences parallèles de la même cause, tandis que l'annulation est une conséquence séquentielle de l'immobilisation.
Quand il y a causalité il y a toujours corrélation :
Et la corrélation dans tout ça ? Et bien on peut la trouver un peu partout. Tout d'abord on la trouve dans toute causalité directe : il y a une corrélation entre le nombre d'accidents de voitures et le nombre d'hospitalisations. On la trouve également dans les causalités indirectes, quoique de manière plus faible : beaucoup d'autres éléments peuvent intervenir (on peut rencontrer une infirmière ailleurs que dans un lit d'hôpital), et limiter la relation.
Quand il y a corrélation il y a toujours causalité :
On peut également trouver une corrélation entre deux conséquences parallèles : on pourrait calculer la corrélation entre le taux d'immobilisation de véhicules et le taux d'hospitalisation. Pourtant il n'y a absolument aucune relation causale directe entre les deux faits : une corrélation montre l'existence d'une causalité, mais ne la précise absolument pas.
Quelle était la causalité dans l'histoire racontée par Watzlawick ? Tout simplement une forte vague de chaleur sur tout le Pacifique, qui avait incité les Américains à augmenter leur consommation de boissons (dont la bière), et qui avait entraîné de graves problèmes sanitaires chez les Japonais pas encore tout à fait remis de la guerre. La corrélation était bien le symptôme d'une causalité.
Du sens de la causalité
Il n'existe qu'un seul pays au monde où la durée de vie des hommes est supérieure à celle des femmes (le Koweït). Doit-on en déduire que les hommes Koweitiens martyrisent leurs femmes au point de renverser la tendance naturelle (durée de vie beaucoup plus longue pour les femmes) ou au contraire que ce sont les femmes de tous les autres pays qui détruisent tellement les hommes qu'elles les font mourir plus tôt ?
Trouver une causalité n'est pas toujours suffisant : encore faut-il en connaître le sens, et ce n'est pas toujours facile. Parfois certaines évidences doivent être remises en cause. Par exemple : les enfants battus apparaissent souvent comme plus désagréables que les enfants non battus. Doit-on en déduire qu'ils sont désagréables parce qu'ils sont battus ou battus parce qu'ils sont désagréables ? (réponse : ça dépend, aucune généralité n'est possible).
Ce problème se pose énormément en génétique du comportement. Et on s'aperçoit de plus en plus que certaines "évidences" sont remises en question, que la causalité n'était pas dans le sens que l'on croyait.
Et je laisse à la sagacité du lecteur le soin de conclure quant à la situation du Koweït...
Une Personne indivisible
Il a été calculé récemment qu'un Caucasien (blanc d'origine Européenne) n'avait qu'une probablité de 28% de battre un Noir (d'origine Africaine) à la course à pieds sur courte distance. Cela signifie que si l'on compare 100 blancs à 100 noirs (en faisant correspondre les âges), les noirs gagneront 72 fois. Qu'en déduire si on ne prend qu'un seul noir ?
Reprenons le même type d'exemple avec la différence de taille entre les hommes et les femmes. On dit qu'une femme fait 20% de moins qu'un homme. Que peut-on en déduire sur une femme précise ? Avant de l'avoir vu on peut imaginer qu'elle sera plus petite qu'un homme moyen de même origine. Mais dès qu'on l'a vu cette différence moyenne ne voudra plus rien dire : elle sera ou non plus grande ou plus petite. Cette moyenne n'impose en rien qu'elle devra faire 20% de moins : elle peut très bien mesurer 1m90. Tout cela semble bien évident : un dé non pipé que l'on jette en l'air tombera équiprobablement sur une des six faces, pas sur 16,67% des 6 faces à la fois !
Pourtant l'expérience montre que cette approche n'est pas très claire pour tout le monde. En effet quiconque cite une statistique (par exemple : les femmes sont en moyenne plus petites que les hommes) prend le risque d'entendre son interlocuteur lui citer un contre-exemple (les Pygmées sont plus petits que les Hollandaises). Et il est tout aussi fréquent de voir quelqu'un tirer d'une statistique (une généralisation) un avis définitif sur un individu, et là c'est beaucoup plus grave.
Reprenons notre premier exemple : ce noir est un individu unique, qui gagnera, ou non, à la course sur courte distance. Le racisme naît souvent de cette généralisation abusive.
Pourcentages Génétiques
A chaque nouvelle découverte sur le pourcentage d'origine génétique d'un comportement, un Albert Jacquard ou un autre se lève pour faire remarquer qu'on ne peut distinguer la part de l'inné de celle de l'acquis dans un comportement, de la même façon qu'on ne peut distinguer la part de chacun des cotés d'un rectangle dans sa superficie. Et pourtant on continue de lire que notre comportement est en moyenne à 50% d'origine génétique. Qu'est-ce-que ça signifie ?
Imaginez que vous calculiez la superficie d'un rectangle : cette superficie est dépendante de la longueur de chacun des deux cotés. Si un de ces cotés est le double de l'autre, peut-on alors dire qu'un coté explique 1/3 de la superficie, tandis que l'autre explique les deux tiers restant ? Non, ça ne signifie rien, et Jacquard a raison sur ce point : il ne répond pas à la question posée.
Imaginez maintenant que vous ayez plusieurs rectangles de longueur et/ou largeur différentes comme sur l'image ci-après:
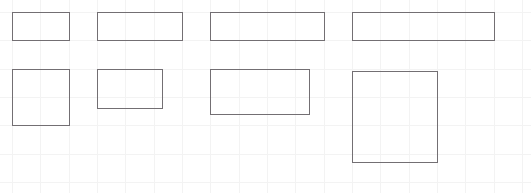
Ils présentent des superficies différentes, et on peut se demander quelle part d'un coté ou de l'autre (longueur et largeur) explique ces différences. Par exemple, sur la première ligne ci-dessus, seul le coté horizontal (la longueur) change : 100% de la différence de superficie entre les 4 rectangles est donc expliquée par la différence de longueur, 0% par la différence de largeur (verticale). Dans la deuxième ligne, les deux cotés varient, et un calcul précis permettrait de distinguer quel part de la variation de superficie est expliquée par la variation d'un coté et de l'autre.
Frans de Waal (Université d'Atlanta) a utilisé une autre image pour expliquer la même différence dans le Pour la science de Janvier 2000 (page 62) :
"Chercher l'influence relative des gènes et de l'expérience acquise dans un trait de caractère est absurde. Le primatologue suisse Hans Kummer a utilisé une métaphore pour l'expliquer. C'est comme si on voulait déterminer qui, du musicien ou de son instrument, produit la musique ou dans quelles proportions ils interviennent. En revanche, si la musique change, on peut légitimement se demander qui, du musicien ou de l'instrument (des gènes ou de l'expérience acquise), a changé. C'est la seule question pertinente."
Et en effet quand Judith Rich Harris annonce une moyenne d'origine de comportement de 50% pour la génétique, 10% pour l'environnement familial, et 40% pour les pairs, elle ne parle que de pourcentage de changement de la Variance.
Dire qu'un comportement est à 50% d'origine génétique n'est donc qu'une simplification (abusive) de langage.
Plus proches des chimpanzés que de nos parents ?
On peut lire que nous partageons 98,5% (ou 97,5%, selon les auteurs) de nos gènes avec les chimpanzés, et seulement 50% avec chacun de nos parents. Comment est-ce possible ?
Là encore il ne s'agit que d'un raccourci de langage : les 50% en provenance de chacun des parents signifient simplement qu'à la conception, la moitié de nos gènes proviennent de notre père, et l'autre moitié de notre mère, pas que ces gènes sont différents.
Exemple simplifié : vous prenez deux sacs remplis chacun de boules noires et mettez dans un troisième sac 50 boules en provenance du premier sac, et 50 boules en provenance du deuxième sac : vous pouvez dire que 50% des boules de ce troisième sac proviennent du premier, et 50% du deuxième, or il n'y a toujours que des boules noires. Si maintenant vous avec un quatrième sac qui contient 97 boules noires et 3 blanches, vous pouvez dire que ces deux sacs sont à 97% identiques.
Philippe Gouillou
10 mars 2000
©Philippe Gouillou - 10 mars 2000



